|
This paper was published in Perception & Psychophysics 1984, 35 (3), 269-278, and is reproduced with permission by the Psychonomic Society, Inc. |
|
 |
| Biopsychology.org | Papers |
The psychophysics of taste from the entropy of the stimulus[*]
|
This paper was published in Perception & Psychophysics 1984, 35 (3), 269-278, and is reproduced with permission by the Psychonomic Society, Inc. |
|
|
During the process of perceiving a steady taste stimulus, information is received, or (information) entropy is reduced. A single equation, the entropy equation, relates three fundamental variablesmagnitude estimate, stimulus intensity, and stimulus duration. From this single equation, we can derive, in principle, all psychophysical relations for a steady taste stimulus, involving these three variables only. A number of examples are given. The Stevens exponent for taste is derived theoretically for certain experimental conditions, using statistical mechanics. Weber's constant is derived in terms of the information transmitted per taste stimulus. The concept of a "surface of perception" is introduced.
INTRODUCTION
The science of psychophysics is replete with empirical equations and experimentally established rules Fechner's logarithmic law, Stevens's power law, Weber's fraction, Miller's channel capacity and many others. In the author's previous publications (Norwich, 1977, 1981a, 1983b), it was shown that many of these seemingly disjoint, empirical rules could be demonstrated to be specific instances of one general principle, that of reduction of uncertainty during the process of perceiving a steady stimulus. A single equation, the equation of entropy, was derived to govern the progressive acquisition of information during the process of perception, and many of the fundamental empirical equations and rules of psychophysics emerged from it. In this paper, we shall show, by way of example, that one can go a long way toward elaboration of the complete psychophysics of taste (involving single, not multiple, stimuli) using only this single equation of entropy and the physical properties of the solutions being tasted. The primary reason for confining this paper to the sense of taste is that the chemical physics of solutions, at least of dilute solutions, is fairly well understood. Moreover, for the modality of taste, physical, neural, and psychophysical events have been correlated in the same subject, a correlation which we shall draw upon.
In the remainder of this introduction, the entropy theory will be summarized. But for more complete understanding, the reader is referred to the three earlier publications cited above.
Fundamentally, the entropy conjecture (and the term "entropy" will always be used here in the information theoretical sense, not in the thermodynamic sense) states that perception can occur only when a state of uncertainty exists concerning some feature of the stimulus. In this paper, as in most of the preceding ones, we consider only the perception of intensity of steady or constant stimuli. Uncertainty about the stimulus will result from fluctuations in the intensity of the stimulus about its mean value. Since stimuli of greater intensity exhibit greater fluctuations about the mean, the resolvable uncertainty (or transmissible information, or entropy), H (bits), as well as the neural response, F (impulses/second), will also be greater. The fundamental hypothesis of the entropy view of perception (Norwich, 1977, 1981a) is that neural response is related to stimulus entropy by means of the equation
For the sense of taste, experiments by Borg, Diamant, Ström, and Zotterman (1967) show that magnitude estimates of stimulus intensity are directly proportional to neural responses. Therefore, we are at liberty to express the psychological magnitude estimate by the variable F, and relate F to the entropy H by Equation 1, where k is now determined by the arbitrary scale units of the experimenter. Throughout this paper, F will refer to the magnitude estimate of a stimulus.
|
|
Figure 1. A stimulus is applied to a sensory receptor and is maintained. If information about the intensity of the stimulus were received completely and instantaneously by the receptor, the process would be described by the upper step function. But the acquisition of information is gradual, as represented by the lower curve. The difference between the amplitudes of the step and the curve defines the decline in uncertainty during the process of perception, and so represents adaptation to the stimulus. |
When a stimulus is applied to a sensory receptor, information is transmitted to the receptor. If the acquisition of information by the receptor were instantaneous, the graph of information receipt with time would have the appearance of a sudden step, as shown in Figure 1. But information is never transmitted instantaneously. The receptor samples its stimulus progressively, and the acquisition of information is gradual, as shown by the curve in Figure 1. The difference between the amplitudes of the step and the curve in the graph in Figure 1 is a declining curve, which traces the progressive reduction in uncertainty and describes the process of adaptation to the stimulus (Norwich, 1981a).
When the entropy function, H, is evaluated for a steady stimulus of mean intensity, m, applied to a sensory receptor for a time duration, t, and this function is introduced into Equation 1, we obtain (Norwich, 1977,1981a)
| (2) |
F = ½ k ln(1 + bmn/t), n, b constants > 0.
Equation 2 is the explicit equation of entropy relating perceived magnitude, F, to the magnitude and duration of a constant, applied stimulus. For the sense of taste, m is the concentration of the solution being tasted. From this equation, one should be able, in principle, to derive all psychophysical functions relating to taste of a single substance, involving the three variables F, m, t, except those involving threshold. It remains for the reader to judge how closely we can approach this goal.
MAGNITUDE ESTIMATION: PREDICTING THE EXPONENT IN STEVENS'S LAW FOR TASTE
The factor mn entered Equation 2 from the physical relationship between the mean and variance of a stimulus (Norwich 1977,1981a),
(for "µ" read "varies as" or "is proportional to"). Since the stimulus magnitude, in this case, is the concentration of a solution, the value of the exponent, n, may be calculated theoretically for experiments in magnitude estimation that are conducted under certain standardized conditions. If the solution being tasted is dilute, and if the tasting process consists of holding the solution on the tongue without flow, then fluctuations in the composition of the solution, s2, are related to the mean or expected composition (concentration), m, by the equation (Landau & Lifshitz 1969; Tolman, 1938):
That is, the value of the exponent, n, is 1.0 from the statistical mechanisms of the dilute, stationary solution. Equation 4 is derived in the Discussion section below.
In an experiment for magnitude estimation, let the stimulus be held for an interval of time, t = t0. We may now substitute A for b/t0 and 1.0 for n in Equation 2:
For dilute solutions. Equation 5 may be expanded in a Taylor series,
For quite dilute solutions, we may retain just the first term of the expansion,
Equation 7 is recognizable as Stevens's law, which may be written more concisely:
For this standardized case, magnitude estimate is proportional to concentration to the first power. That is, in experiments involving magnitude estimation of concentrations of dilute solutions, where the solution is kept stationary in the mouth, the exponent in Stevens's law is expected to be 1.0. This result is largely independent of any mechanism of action of the sensory papillae, and depends only on the entropy conjecture and the physics of solutions. This will be examined in greater detail in the "Discussion" section below.
|
| Figure 2. Deviation from Stevens's law for the sense of taste. m is the stimulus concentration and F is the magnitude estimate. The dashed line depicts the simple power law for taste (n = 1). The curve, which deviates progressively from the line for larger m, is predicted from the entropy function, and has been observed experimentally. |
Equation 8 is expected to govern the perception of taste for only very dilute solutions. For more concentrated solutions (larger values of m), we can retain the first two terms of the Taylor expansion:
F = ½ kAm - ¼ kA2m2
or simply
| (9) |
The second term on the right-hand side will become prominent only for larger values of the concentration, m. Therefore, a graph of magnitude estimate, F, against concentration, m, is expected to deviate progressively more from linearity with increasing concentration, as shown in Figure 2. This deviation from linearity is seen very clearly in most of the experimental graphs for taste given by Stevens (1969). Equation 9 was derived by Norwich (1977, 1981a) with reference to electrical activity in sensory neurons.
The ratio of change in stimulus intensity to mean stimulus intensity, Dm/m, required to produce one just noticeable change in perceived intensity, DF, is known as the Weber fraction. Various empirical equations describing the relationship between Weber fraction and stimulus intensity have been proposed. We can, however, derive such a relationship directly from the entropy Equation 2 with A = b/t.
Differentiating both sides with respect to m,
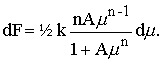
Replacing the differentials by finite differences, dividing by m, and rearranging the equation,
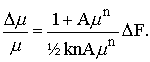
Replacing (½ knA)-1
by the single constant, D, we have
If we associate DF with the small change in magnitude estimate corresponding to one just noticeable difference in perceived intensity, Equation 10 will be a general expression for the Weber fraction.
If Fechner's supposition is valid for the sense of taste that is, that DF is the same for all F we may then set DF equal to a constant (say DF = 1, since it depends only on the arbitrary scale of measurement of subjective magnitudes). Taking the value n = 1 for taste, Equation 10 becomes simply
or equivalently,
|
| Figure 3. Weber fraction, Dm/m, for taste as a function of stimulus concentration, m. Fechner's conjecture (see text) introduced into the entropy equation produces the function described by the upper, dashed curve, which approached a constant asymptote. Relaxation of Fechner's conjecture (see Appendix) gives rise to the lower, solid curve, which reaches a minimum and then rises. Such a curve has been found experimentally. |
This form of the equation for the Weber fraction has been proposed empirically by Fechner and for auditory noise by Miller (1947). Equations 11a and 11b explain the familiar shape of the graph of Dm/m, as shown in the upper curve in Figure 3.
It is instructive that Ekman (1959), beginning with a form of Stevens's law, and relating DF to F from experiments on weight lifting, derived Equation 11 in a manner very similar to the one given above.
Fechner's supposition may not be valid for taste. Stevens (1936; pure tones) and Miller (1947; white noise) discovered that just noticeable differences are unequal in subjective magnitude. For sound,
where L is loudness and N is the number of distinguishable steps. If a relationship such as Equation 12 for sound existed for taste, the form of the graph of Dm/m vs. m would be altered slightly: the curve would reach a minimum and then rise somewhat, as shown by the lower curve in Figure 3. This curve is of the type actually observed by Holway and Hurvich (1937). The mathematical derivation of its equation is given in the Appendix.
Again, the various empirical equations for a psychophysical function have been derived in a meaningful way from the equation of entropy for a constant stimulus. Only one principle is invoked (although some constraint on AF is required).
When a taste stimulus of constant magnitude is applied and held in place, the subject adapts to the stimulus. Magnitude estimates diminish progressively with time. Since concentration, m, does not change with time in this experiment, we may replace bmn by the positive constant, B, so that Equation 2 simplifies to
Equation 13 describes the progressive fall in magnitude estimate, F, with time, t. By curve-fitting the data from experimental adaptation curves to the function given by Equation 13, we can evaluate the constants k and B, and hence, by the method described earlier (Norwich, 198la), measure the information transmitted per taste stimulus.
Very briefly, let us review the procedure:
(1) Curve-fit, and thus evaluate k and B.
(2) Measure the maximum and minimum magnitude estimates made by subject, Fmax and Fmin.
(3) Using Equation 1, calculate the change in entropy (= information transmitted) during the time of perception of the stimulus:
If we make our calculation from Equation 14 for a relatively strong stimulus, DH will approach the channel capacity for taste a quantity usually measured by means of a test of categorical judgments.
Consider, for example, the experimental data on taste adaptation obtained by Gent and McBurney (1978). Using the most intense sucrose stimulus (1.0 M) and fitting the data from Gent and McBurney's Figure 2 to Equation 13, we obtain
That is, k = 7.40. We read from the data, Fmax = 11.5, Fmin = 1.0. Using Equation 13, we calculate that the information transmitted in the perception of a sucrose stimulus may be at least as great as
The corresponding value of channel capacity for sucrose measured by Beebe-Center, Rogers, and O'Connell (1955) is 1.69 bits, which differs by 17% from the former calculation. A similar calculation may be carried out for 1.0 M NaCl solution. Using data from Gent and McBurney's Figure 1, we obtain
With k = 8.20, Fmax = 11.76, Fmin = .40, the information transmitted in the perception of a saline solution may be at least as great as
The value measured by Beebe-Center et al. for NaCl from categorical judgment experiments is 1.70 bits per stimulus, differing by 15% from the former estimate.
We see that adaptation effects and limitations on categorical judgments are phenomena that are unified and cohere within the entropy view of perception.
For larger durations of stimulus application, Equation 2 may again be approximated by the first term of a Taylor expansion (with n = 1 for taste):
For F = FD = some arbitrary, low level of sensation, t = tD, where
tD = ½ k bm/FD.
That is, decay time for taste sensation is proportional to the magnitude (concentration) of the stimulus.
Thus, we have derived the result found experimentally by Krakauer and Dallenbach (1937) and by Abrahams, Krakauer, and Dallenbach (1937).
Let us now proceed with a more detailed analysis of the examples given above.
It has been argued here that at the core of psychophysics lies a single theme: Magnitude estimates of simple, constant stimuli are equal to the entropy of these stimuli as perceived by the receptor. The entropy is a function of the two variables, stimulus magnitude and time. The expression for entropy is derived from a model of the perceptual process, and is given by Equation 2. This expression contains three parameters k, b, and n. The first parameter, k, is determined by the experimenter's arbitrary scale for magnitude estimates. The second, b, involving noise within the sensory receptor, cannot yet be predicted. The third parameter, n, which emerges as the exponent in Stevens's power law, can be predicted or evaluated a priori for the sense of taste.
For a constant taste stimulus, consisting of a dilute solution held without flow in contact with the tongue, the stimulus entropy derives from fluctuations in the local density of solute. (It is important to recall that we refer to the entropy of information, not to thermodynamic entropy.) The relationship between the magnitude of these fluctuations, s2, and the mean solute density or concentration, m, has been derived within statistical mechanics using the notion of a grand canonical ensemble. In order to minimize confusion in nomenclature, let us use the symbol c instead of \n. for concentration. From Tolman (1938, Equation 141.43), we write
where R is the gas constant, T is the absolute temperature,
m is the chemical potential,
is the mean number of molecules present in some volume of solvent, and N is the number of moles within the
volume. From physical chemistry, we have, for non-electrolytes (Kirkwood &
Goldberg, 1950),
where the activity coefficient, g, is a function of c, while
is a function only of temperature and
pressure. (The corresponding expression for an electrolyte is a little more
complicated.) Differentiating partially with respect to c,
For dilute solutions, the final term is expected to be small, so that
Finally, introducing Equation 19 into Equation 16 leaves
or, reverting to the symbol "m" for concentration, s2 µ m, as stated in Equation 4. An electrolyte that is completely dissociated will lead to a similar result.
Since Equation 2 has been derived making use of the relationship s2 µm (Norwich, 1977), we can now set n = 1. When Equation 2 was expanded in a Taylor series, we were able to identify n with the exponent in Stevens's law.
We see, therefore, that, to a first approximation, the Stevens index for the sense of taste is 1.0. This emerges from considerations of thermodynamics and statistical mechanics. It does not involve any particular mechanism that may operate within the sensory receptor.
For larger concentrations, the final term in Equation 18 may not remain negligible, which may produce a change in the theoretical value of the Stevens index from 1.0. For an electrolyte, g, and hence the final term, may be evaluated from the Debye-Hückel theory. This may explain in part the variation in the value of the index found experimentally. However, we shall not pursue the matter further here.
One should not attempt to equate s2 in Equation 3 with the variance of a sinusoidal stimulus, for example, a tone of varying intensity. This is not the correct sense, s2 is associated with microscopic, not macroscopic, fluctuations.
We have considered theoretically only the case where subjects sampled solutions that were at rest (zero flow) on their tongues. This restriction was made because the derivation of Equation 4 was for thermodynamic equilibrium. Perhaps the best method for achieving this state experimentally is that of Gent and McBurney (1978), who apply a pledget of filter paper to the surface of the tongue. The "sip" technique and the "flow" technique will obviously not produce zero flow. This, too, may contribute to a deviation between theoretical and experimental values of Stevens's index. Meiselman, Bose, and Nykvist (1972) have compiled a table of power-law exponents measured by various investigators between 1960 and 1971. For magnitude estimation, the geometric means of these exponents were reported as: NaCl, .91; quinine hydrochloride, .85; sucrose, .93; and hydrochloric acid, .99. These values are quite close to the value of 1.0 suggested by Equation 4. Although there is a good deal of variation in the values reported for these exponents, the results are not inconsistent with the theoretical value of 1.0. For example, the arithmetic mean of the values reported for sodium chloride is 1.04 ± .10, and the arithmetic mean for hydrochloric acid is 0.98 ± .13. Neither exponent is significantly different from 1.0.
Deviations from Stevens's simple power law have recently been studied in some depth by Atkinson (1982). He has demonstrated in this carefully documented study that deviations can be observed not only for taste, but for other modalities, such as vision and audition, as well. Atkinson has shown that F vs. m curves (where F may be impulse frequency or magnitude estimate) may be better described by multiplying the simple power function by a modulating exponential function, which he terms internal masking. In our current symbols,
is Atkinson's equation governing taste.
In the present study, we acknowledge the same type of systematic deviation from a simple power law, but we attribute it to the natural form of the entropy function, tending with greater m from linear to logarithmic dependence on m, rather than to a specific masking process.
Deviations from the simple power law for the sense of taste were, in retrospect, predicted even in 1954 by Beidler's well-known equation relating stimulus concentration, c, to response, R. Beidler's equation is usually written in the form
However, this equation can be rearranged (Beidler, 1971) into the form
For small values of Kc, the right-hand side may be expanded using the binomial theorem,
If we retain only terms of the first and second degree, Beidler's Equation 23 is identical in form to Equation 9 of the entropy theory, and predicts a progressive deviation from Stevens's law for larger concentrations.
As discussed above, the entropy approach to sensory perception does not provide a molecular mechanism for the transduction of sensory events, such as that suggested by Beidler. The entropy approach is akin to a thermodynamic law: it places constraints upon the nature of events, but does not posit the physical form that these constraints may assume. For example, in applying the entropy equation to calculate the maximum information transmissible to a sensory receptor perceiving a steady stimulus, we made use of a conservation of information constraint for the receptor-stimulus system: maximum information transmissible to the receptor = total uncertainty (entropy) associated with fluctuations of the stimulus. No mechanism, just a constraint.
The derivation of the mathematical form of Weber's fraction from entropy considerations is interesting from various points of view. It permits us to understand why the function takes on its characteristic form, and, moreover, it demonstrates graphically the merging of Weber's with Stevens's law. Weber's original thesis stated that Dm/m = a constant (see, e.g., the clear historical account by Baird & Noma, 1978). This is the situation that prevails experimentally when m is large. The required result is obtained mathematically from Equation 10 by taking the limiting case for large m:
But when the stimulus is weaker (m smaller), the first term on the right-hand side of Equation 10, Dm-n, gains prominence and the Weber fraction is far from constant. The exponent -n is, curiously enough, the negative of Stevens's exponent. So we see that the Weber fraction is equal to the sum of two terms, one that issued from Weber's intuition and one that issued from Stevens's power law.
The informational approach permits us to discern relationships between psychophysical variables that were not otherwise evident, such as the following relationship between Weber's constant and the channel capacity for taste information. From Equation 1
so that
From Equations 24 and 26,
|
|
| Figure 4. Surface of perception for a steady stimulus. m is the stimulus magnitude and t is the stimulus duration. H (or F) represents the magnitude estimate. Planes parallel to the mH plane intersect the surface of perception to define curves of magnitude estimation. Planes parallel to the tH-plane intersect the surface to define adaptation curves. The maximum amplitude of these adaptation curves is equal to the information transmitted per stimulus. |
If H is taken to be the information transmitted by a large stimulus, then F/DF is the total number of jnds in this stimulus (since DF is taken to be constant here). Therefore, from Equation 27,
Information per stimulus (bits) =
| (28) |
The factor of ln 2 is required to give the information in bits. We can now evaluate the right-hand side of Equation 28 using the data of Holway and Hurvich (1937), and compare the result to the known information transmitted by a large, saline, taste stimulus.
The method for measuring the total number of jnds making up a stimulus was devised by Miller (1947) [1]. Let Dm be the change in stimulus intensity corresponding to one jnd. Dm will, in general, change with m. The total number of jnds in a large signal of intensity m1 is given by the integral (Miller, 1947, Equation 7)
| (29) |
where m0 is the intensity of the smallest perceptible taste stimulus. This integral is numerically equal to the area under the curve obtained by plotting 1/Dm against m. Such a graph was plotted by Holway and Hurvich (1937, Figure 9), and their data are also given in tabular form. It is, therefore, a simple matter to replot their graph and measure the area under the curve between the limits m0 = .025 M to m1 = 4.00 M. (The approximation expressed by Equation 19 is weaker for the more concentrated solutions near m1, but we shall retain it anyway.)
We can now assemble the measured data and test Equation 28. For taste, let us take the Stevens index, n, equal to 1.0. Weber's constant from Holway and Hurvich's (1937) Figure 8 is approximately equal to 0.28. Total jnds measured from Holway and Hurvich's Figure 9 by the method described above is equal to 9.66. Therefore, the right-hand side of Equation 28 is equal to
The left-hand side of Equation 28 has been calculated before from the data of Gent and McBurney (1978) and is equal to 2.00 bits per stimulus (or by Beebe-Center et al. as 1.70), so that the two sides of the equation are very nearly equal, as required.
Gent and McBurney (1978) have fitted their adaptation data to a single exponential function, and the data are fitted quite well. These authors do not presuppose a model of the adaptation process.
Equation 13 has been derived from the entropy principle using a model in which a sensory receptor samples its stimulus at regular intervals. This assumption may not be completely valid, but it permits us to make reasonably accurate calculations of the amount of information transmitted per stimulus. It is quite interesting to observe that merging the two approaches to the adaptation curve permits rapid approximation of the amount of transmitted information. As shown in a previous paper (Norwich, 1981a), this quantity may be approximated by calculating the quantity
, where t1 is the time of the highest magnitude estimate of a given stimulus and
t2 is a measure of the time of decline of the adaptation curve. If we take
t1 to be Gent and McBurney's first sample time of 5 sec (somewhat less than the shortest reaction time measured by Holway & Hurvich, 1938, but in keeping with the data of Corso, 1967), and
t2 to be estimated by their exponential time constant, we may then make the following calculations:
| Sucrose: | t1 = 5. sec, t2
= 60. sec, = 1.8 bits per stimulus. |
| NaCl: | t1 = 5. sec, t2
= 71. sec, = 1.9 bits per stimulus. |
These results are quite close to the other, more exact estimates.
The use of the entropy equation 5, 13 to govern both the neural and psychophysical adaptation processes is justified by the work of Borg et al. (1967), who showed that the two operated in parallel during the process of magnitude estimation of taste stimuli. The universality of this principle has, however, been properly questioned by Sato (1971). In this paper, we have taken the position that the same equation will hold for both neural and psychophysical processes, with different values for the constant, k.
Implicit in this study, and in other modern studies of perception, is the importance of regarding the magnitude of sensation as a function of the two independent variables, stimulus magnitude and stimulus duration [2]. That is, F or H should be regarded as a function of both m and t. Graphically, this gives rise to a surface of perception. Such a surface is drawn in Figure 4 for a steady stimulus. The intersections of the surface with planes parallel to the tH-plane are adaptation curves, each curve corresponding to a different, constant stimulus magnitude. The intersections of the surface with planes parallel to the mH-plane are curves of magnitude estimation, each curve corresponding to a different degree of adaptation (stimulus duration).
The surface of perception has been drawn with reference to Equation 2. Fundamentally, in this paper, we have tried to show that the sense of taste is governed by a particular surface with n = 1, a constraint derived from chemical physics, and that, from the geometry of this surface, can be derived, in principle, all psychophysical relationships involving the variables F (= kH), m, and t. Mixtures or comparisons of different qualities of stimuli, cross-modality matching, thresholds, esthetics, and temperature effects have not been treated here. Receptors are unadapted to their stimulus at t = 0.
Rather a large number of predictions emerge from Equation 2. For example, if an experiment involving magnitude estimation is conducted by applying stimuli of varying intensities, each for the same time duration, and then, on the same subject, an experiment involving adaptation is conducted by applying stimuli of the same magnitude for varying durations, the same Equation 2 is expected to account for the results of both experiments. The expected values of the parameters k and b are the same for both experiments. Remember, though, that the receptors must be completely unadapted to their stimuli at zero time.
Figure 5 summarizes what has been derived from the entropy equation 2.
|
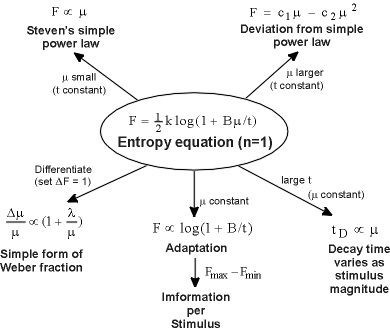
| Figure 5. The psychophysics of taste from the entropy of the stimulus. All phenomena shown here can find their explanation in the entropy equation. The arrows show how this equation has been utilized to make each derivation. |
(1) When m is small and t is constant, Stevens's power law for taste results from a Taylor expansion.
(2) When m is less small and t is constant, the observed deviation from Stevens's simple power law for taste results from a Taylor expansion.
(3) Differentiating Equation 2, we obtain the observed form of the Weber fraction for taste.
(4) When m is constant, we obtain the adaptation curve, which defines two constants, t1 and t2. The information transmitted per taste stimulus is approximately equal to ½ the logarithm of their quotient.
(5) When m is constant and t is large, we find that the decay time of taste adaptation is proportional to the stimulus magnitude.
"Oneness" is the fundamental theme of this paper. Many apparently dissociated phenomena of psycho-physics are seen to be linked together into one organic whole. The principle that provides unity to the whole is the principle of the relativity of perception: perception is relative to the expectation of the perceiver. To perceive is to be uncertain, to entertain multiple expectations. The psychophysical laws we have treated deal with the resolution of uncertainty (by which is meant the gain of information), a process that has been modeled for a steady stimulus by Equations 1 and 2. The manner by which this uncertainty may be set up, or "doubt" established, and some of its unanticipated consequences are discussed by the author elsewhere (Norwich, 1983a, 1983b).
The mechanism of a sensory receptor cannot be inferred from considerations of entropy alone. However, an interesting model involving energy detection by organic superconductive microregions has been postulated by Cope (1981); it leads to some of the same conclusions as the entropy approach (Norwich, 1981b).
Finally, it must be recalled that the introduction of information theory as an integral part of psychophysics was suggested by Baird (1970a, 1970b). While many people have made calculations on the information capacity of neurons, etc., Baird was among the first to weave information theoretical concepts into the fabric of perceptual theory. The work of Moles (1958/1966) may also be seen to anticipate the relationship explored in the present work between stimulus entropy and Fechner's law.
ABRAHAMS, H., KRAKAUER, D., & DALLENBACH, K. M. (1937). Gustatory adaptation to salt. American Journal of Psychology, 49, 462-469.
ATKINSON, W. H. (1982). A general equation for sensory magnitude. Perception & Psychophysics, 31, 26-40.
BAIRD, J. C. (1970a). A cognitive theory of psychophysics. I. Information transmission, partitioning, and Weber's law. Scandinavian Journal of Psychology, 11, 35-46.
BAIRD, J. C. (1970b). A cognitive theory of psychophysics. II. Fechner's law and Stevens' law. Scandinavian Journal of Psychology, 11, 89-102.
BAIRD, J. C., & NOMA, E. (1978). Fundamentals of scaling and psychophysics. New York: Wiley.
BEEBE-CENTER, J. G., ROGERS, M. S., & O'CoNNELL, D. N. (1955). Transmission of information about sucrose and saline solutions through the sense of taste. Journal of Psychology, 39, 157-160.
BEIDLER, L. M. (1954). A theory of taste stimulation. Journal of General Physiology, 38, 133-139.
BEIDLER, L. M. (1971). Taste receptor stimulation with salts and acids. L. M. Beidler (Ed.), Handbook of sensory physiology: Vol. 4. Chemical senses. 2. Taste. Berlin: Springer-Verlag.
BORG, G., DIAMANT, H., STRöM, L., & ZOTTERMAN, Y. (1967). The relation between neural and perceptual intensity: A comparative study on the neural and psychophysical response to taste stimuli. Journal of Physiology, 192, 13-20.
COPE, F. W. (1981). On the relativity and uncertainty of distance, time and energy measurements in man. Physiological Chemistry and Physics, 13, 305-311.
CORSO, J. F. (1967). The experimental psychology of sensory behavior, New York: Holt, Rinehart & Winston.
EKMAN, G. (1959). Weber's law and related functions. Journal of Psychology, 47, 343-352.
GENT. J. F., & MCBURNEY, D. H. (1978). Time course of gustatory adaptation. Perception & Psychophysics, 23, 171-175.
HOLWAY, A. H., & HURVICH. L. M. (1937). Differential gustatory sensitivity to salt. American Journal of Psychology, 49, 37-48.
HOLWAY, A. H., & HURVICH, L. M. (1938). On the psychophysics of taste: I. Pressure and areas as variants. Journal of Experimental Psychology, 23, 191-198.
KIRKWOOD, J. G., & GOLDBERG, R. J. (1950). Light scattering arising from composition fluctuations in multi-component systems. Journal of Chemical Physics, 18, 54-57.
KRAKAUER, D., & DALLENBACH, K. M. (1937). Gustatory adaptation to sweet, sour, and bitter. American Journal of Psychology, 49, 469-475.
LANDAU, L. D., & LIFSHITZ, E. M. (1969). Statistical physics. Oxford: Pergamon.
MEISELMAN, H. L., BOSE, H. E., & NYKVIST, W. F. (1972). Magnitude production and magnitude estimation of taste intensity. Perception & Psychophysics, 12, 249-252.
MILLER, G. A. (1947). Sensitivity to changes in the intensity of white noise and its relation to masking and loudness. Journal of the Acoustical Society of America, 19, 609-619.
MOLES, A. (1966). Information theory and esthetic perception (J. E. Cohen, Trans.). Urbana: University of Illinois Press. (Original work published 1958.)
NORWICH, K. H. (1977). On the information received by sensory receptors. Bulletin of Mathematical Biology, 39, 453-461.
NORWICH, K. H. (1981a). The magical number seven: Making a "bit" of "sense." Perception & Psychophysics, 29, 409-422.
NORWICH, K. H. (1981b). Uncertainty in physiology and physics. Bulletin of Mathematical Biology, 43, 141-149.
NORWICH, K. H. (1983a). To perceive is to doubt: The relativity of perception. Journal of Theoretical Biology, 102, 175-190.
NORWICH, K. H. (1983b). Perception as an active process. Mathematics and Computers in Simulation, 24, 535-539.
SATO, M. (1971). Neural coding in taste as seen from recordings from peripheral receptors and nerves. In L. M. Beidler (Ed.), Handbook of sensory physiology: Vol. 4. Chemical senses. 2. Taste. Berlin: Springer-Verlag.
STEVENS, S. S. (1936). A scale for the measurement of a psychological magnitude: Loudness. Psychological Review, 43, 405-416.
STEVENS, S. S. (1969). Sensory scales of taste intensity. Perception & Psychophysics, 6, 302-308.
TOLMAN, R. C. (1938). The principles of statistical mechanics. Oxford: Oxford University Press.
THE WEBER FRACTION: BASIS FOR THE LOWER CURVE IN FIGURE 3
If a relationship such as the Stevens-Miller equation 12 for loudness were valid also for the sense of taste, the equation for the Weber fraction would change somewhat from the form of Equation 11. Suppose that for taste we also found (as did Stevens and Miller) that
F µ Nm,
where F is the magnitude estimate, N is the number of just noticeable differences (above threshold), and m is a constant whose value lies between 2 and 3. Then
N µ F1/m.
Differentiating,
DN µ F1/m-1DF
or
DF µ DN × F1-1/m.
But for the sense of taste
F µ m, |
(8) |
so that
DF µ DN × m1-1/m.
But for one just noticeable difference, we must have
DN = 1,
so that the change in magnitude estimate, DF, corresponding to one just noticeable difference is given by
DF µ m1-1/m.
The latter equation is just the analog of Miller's statement for audition: "A just noticeable difference at a low intensity produces a much smaller change in the apparent loudness than does a just noticeable difference at a high intensity" (Miller, 1947, p. 609). Clearly, for Fechner's original conjecture (see main text), m = 1, so that DF is constant. However, taking m = 2.5, to approximate its value for audition, we find
DF µ m.6.
Introducing this value for DF into Equation 10 in place of the Fechner supposition, and again setting n = 1 for the sense of taste, we obtain in place of Equation 11a,
|
|
(11c) |
The Weber fraction, Dm/m, as described by Equation 11c, is very large for small values of concentration, m, dips to a minimum value, and then rises gently. This is the shape of the lower curve shown in Figure 3, and corresponds to the shape obtained experimentally by Holway and Hurvich (1937).
The assumptions involved in deriving Equation 11c are those of the entropy equation 2 plus the varying subjective magnitude to the difference limen, F µ Nm.
[*] This work has been supported by a grant from the Natural Sciences and Engineering Research Council of Canada. The author is most grateful to Professor R. E. Kapral for his aid and reassurance in matters of theoretical chemistry, and to Diane Meschino for technical help rendered. The author is associated with the Institute of Biomedical Engineering and the Department of Physiology of the University of Toronto. His mailing address is: Institute of Biomedical Engineering, Rosebrugh Building, University of Toronto, Toronto, Ont., Canada M5S 3G9.
Notes after paper publication:
[1] Equation (29) has been attributed to Miller (1947). Later, I found that it was developed at least as early as 1907. It was used by P.G. Nutting, 1907. "The complete form of Fechner's law", Bulletin of the Bureau of Standards, 3, 59-64.
[2] The document uses the term "stimulus duration". I should really have used "time since onset of stimulus". It will only matter for very brief stimuli.
The author is grateful to Dr. Esteban Barrull and to Biopsychology.org for the many efforts extented to make this paper available to readers via the internet.
© Copyright 1984 Psychonomic Society, Inc.
 |
|
A, D > 0,
